La mano derecha

¿Qué parte de tu propio cuerpo no puedes tocar con la mano derecha?

Respuesta a la adivinanza

Haz clic en el siguiente enlace para acceder a la solución del enigma antes de dislocarte la muñeca:

Solución de "La mano derecha" [Clic aquí para acceder]

Jacob Sierra Díaz

El mundo y el amor

Jacob Sierra Díaz

Post-it app

Para los amantes de los Post-it, aquellos que escriben sus ideas en un pequeño trozo de papel cuadrado amarillo (o de otros colores) y que tengan un sistema operativo iOS, y (recientemente), macOS o Android, están de enhorabuena. La aplicación para escribir y dibujar de forma digital en una infinidad de post-it ha llegado. La famosa compañía 3M ha desarrollado una aplicación muy especial para que allá donde vayamos tengamos disponible nuestras notas escritas en post-it digitales. Además, gracias a las últimas actualizaciones es posible acceder a nuestro iCloud para ver todas nuestras notas incluso cuando estemos usando un ordenador distinto al nuestro y con un sistema operativo distinto a macOS (por ejemplo Windows) o pedir a Siri que cree una nota en un nuevo tablón. ¡Comprobemos cómo funciona!

1.- Aprendiendo a usar Post-it en el iPad, iPhone o dispositivos Android

El iPad y iPhone fueron los primeros dispositivos en los que se lanzó esta aplicación. Recientemente Post-it también está disponible en uno de los sistemas operativos móviles más usados alrededor del mundo: Android. A pesar de que en este artículo se ha usado un iPad para exponer sus características principales, las funciones son similares en el resto de dispositivos Android. 

Post-it es una aplicación muy sencilla de usar. Tan sencilla, que al leer este artículo  tendrás la capacidad de usarla de manera autónoma y sin necesidad de recurrir a  las guías de ayuda.

Esta aplicación usa el concepto de canvas (lienzo). Pero Post-it le ha cambiado el nombre a board (tablón), el cual es más adecuado para esta aplicación. Pero, ¿en qué consiste este concepto? El concepto de canvas consiste en simular un lienzo o tablón virtual para nuestros aparatos electrónicos, como si de un corcho de noticias físico con chinchetas se tratase. Como podemos observar en la siguiente captura de pantalla, en nuestros tablones virtuales podremos crear todos los post-it que queramos, moverlos donde deseemos y agruparlos en subgrupos según nuestras inquietudes, necesidades o ideas.

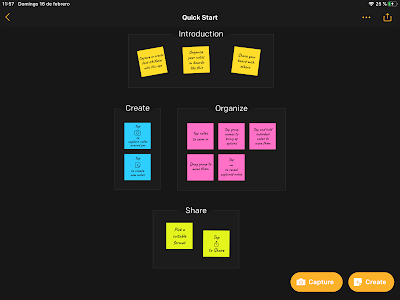
La primera vez que abrimos la aplicación, nos encontraremos el menú de tablones (boards). Aquí aparecerán todos los tablones que hayamos creado. Al abrir la aplicación por primera vez, nos aparecerán tres tablones de bienvenida en el que nos cuentan cómo sacar el máximo partido a la aplicación. Para acceder a un tablón, basta con tocarlo. Para comenzar a escribir en un nuevo post-it, le daremos al botón Create.

La siguiente pantalla que nos aparece después de haber pulsado el botón Create es un post-it en blanco para poder escribir o dibujar en él. Podemos escribir de dos maneras distintas: (a) con los cuatro rotuladores que tenemos o (b) con el generador de textos. Además, podremos cambiar el color del post-it en el botón de Note.

Si le damos al botón Add, el Post-it nos aparecerá en el menú de tablones (boards) suelto. Si le damos al botón Add+ nos aparecerá un nuevo post-it y el que hemos escrito lo llevará al menú de tablones en un mismo grupo.

En el menú de tablones (boards) podemos cambiar el nombre de cada tablón pulsando sobre el mismo y volviendo a pulsar en Show in board. A continuación se nos despliega un menú con la opción de eliminar el Post-it, renombrar el grupo al que pertenece o las opciones de movimiento del grupo de Post-it.

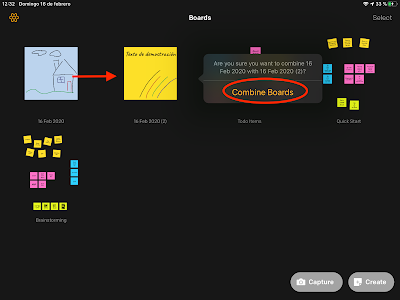
Además, podemos fusionar varios post-it en un mismo tablón. En el menú de tablones (boards) bastará con arrastrar un post-it a otro para ponerlo en un tablón común, confirmando la combinación. Este mismo principio se aplicará también para agrupar a los post-it dentro de un mismo tablón en distintos grupos. El tablón se llamará de manera automática la fecha en la que se ha creado. Pero se puede cambiar el nombre con pulsar la fecha, poner el nombre que queramos y pulsando en el botón Done.

Otra de las funciones más importantes de esta aplicación es la posibilidad de digitalizar nuestros post-it reales en un tablón digital como los que hemos visto. Para ello, simplemente basta con pulsar en el botón Capture (al lado del botón Create) y hacer una foto de dos segundos a nuestros post-it. ¡Incluso si el post-it está girado, lo digitalizará girado (el giro se puede cambiar digitalmente también)! Cabe destacar que para digitalizar post-it, debemos usar la propia marca Post-it, ya que si no, no reconocerá las notas adhesivas de otras compañías.

Aunque hemos visto las cosas básicas que se pueden hacer con esta gran aplicación, aún quedan muchas más cosas nuevas por descubrir. Y seguramente, muchas más actualizaciones y mejoras que 3M implementará en el futuro. Como la mejor forma de aprender es "jugando", te animamos a que instales esta aplicación (totalmente gratuita y, por el momento, sin limitaciones -16 de febrero de 2020-) y descubras todas las funciones que Post-it tiene para ti. Sin embargo, hay un punto un poco negativo para los hablantes del español. Post-it aún no está traducida al castellano. Este hecho no nos debe asustar, ya que las palabras que usa son muy sencillas e intuitivas (por ejemplo, Cancel que significa cancelar una acción en inglés es muy similar al español).

2.- Aprendiendo a usar Post-it en Macintosh

Ahora ya es posible tener la aplicación en Mac y sincronizarla con la nube de Apple (iCloud). Las funciones en los ordenadores de la manzana mordida son muy similares a las que hemos visto en el apartado anterior:

Tenemos dos formas de crear un nuevo Post-it: (a) hacer clic en el icono de crear nuevo post-it (imagen de arriba) o (b) en el menú de arriba en File hacer clic en Create a new note. Observemos que la ventana para escribir y editar un nuevo post-it es muy similar a la ventana que teníamos en los dispositivos móviles. ¿Sabías que también puedes añadir emojis? En el menú de arriba ve a Edit (editar) y a Emoji & Symbol.

Al igual que ocurre con la aplicación en los dispositivos móviles, es posible compartir o exportar nuestras notas en distintos formatos: post-it (si se usa el mismo programa), pdf (para el resto de equipos), Excel o Power Point entre otros. Para compartir un tablón simplemente hay que hacer clic al icono de compartir (cuadrado con la flecha hacia arriba; mira la siguiente captura de pantalla) y seleccionar el formato con el que deseemos exportar el tablero.

Para borrar un tablero, basta con salir al menú de tableros y hacer clic con el botón derecho del ratón (o pulsar sobre el trackpad con dos dedos) y darle a la opción Delete (borrar en inglés). Por otro lado, podemos imprimir un tablero haciendo clic (en el menú de arriba) en File (archivo) y luego en Print (imprimir en inglés). A continuación, en la primera opción, en Printer (impresora) debemos dar a Add Printer... (añadir impresora) para establecer conexión con nuestra impresora y enviar el tablero a imprimir.

En definitiva, esta aplicación es una de las mejores para el tratamiento de post-it digitales y para mejorar nuestra productividad (siempre y cuando nuestra forma de trabajar sea a través de notas adhesivas). ¿Quieres saber más sobre esta aplicación? No dudes acceder a su página web (está en inglés). También puedes escribeir comentarios debajo de esta entrada.

Post-it app. Página web oficial [en inglés] (clic aquí)

Sistemas compatibles: App Store (iPad y iPhone), Mac App Store (ordenadores Apple) y Google Play (dispositivos Android).

Tabla propia de especificaciones

¡Una gran aplicación gratuita para mejorar tu productividad! Muy recomendada para los amantes de las notas adhesivas. De momento está en inglés, pero seguramente con nuevas actualizaciones de los desarrolladores, la podremos disfrutar en nuestro idioma muy pronto. ¡Te encantará!

Jacob Sierra Díaz

San MateValentín-20 con Quick Graph

Hoy es día 14 de febrero de 2020. Es el día de los enamorados. Con ayuda de las matemáticas y las nuevas tecnologías vamos a dibujar un precioso y simétrico corazón en nuestro iPhone o iPad.

Lo primero que debes hacer es descargarte la aplicación Quick Graph desde la App Store. Si eres usuario de Android u otro sistema operativo, existen aplicaciones similares que también puedes usar.

Una vez dentro, veremos que hay un eje cartesiano, una columna a la izquierda y un menú arriba. En la parte superior derecha hay un icono +. Este es el icono para introducir las siguientes funciones:

• y = √(1 - (x-1)·(x-1))

• y = -5/2 · (√(1 -√(x/2)))

• y = -5/2 · (√(1 -√ (-x/2)))

• y = √(1 - (-x-1)·(-x-1))

Automáticamente se representa el conjunto de funciones que hemos definido y que forman un bonito corazón. Puedes cambiar el color a cada función. La aplicación permite enviarlo a la persona en la que estabas pensando mientras lo diseñabas.

¡Feliz día de San Valentín!

Jacob Sierra Díaz

¿Qué tipo de ave eres?

Jacob Sierra Díaz

SOLUCIÓN. El curioso caso de tres socorristas

Si quieres acceder al enunciado antes de leer la solución, haz clic en el siguiente enlace:

Enigma del curioso caso de tres socorristas (clic aquí)

En resumen, ¿cómo es posible que Salvador asegure que no tiene hermanos si dos socorristas dicen que son su hermano? 

¡Veamos la solución!

Salvador no miente. En realidad, Salvador es muy meticuloso. Salvador no tiene tres hermanos; tiene tres hermanas que son socorristas. Así pues las hermanas socorristas sí que pueden decir que tienen un hermano, pero Salvador tiene que decir que tiene dos hermanas (y, por lo tanto, no tiene ningún hermano).

Con este juego aprendemos que a veces es muy importante usar los artículos para evitar confusiones en nuestro receptor del mensaje.

Jacob Sierra Díaz

El curioso caso de tres socorristas

Tres socorristas tienen un hermano llamado Salvador. Sin embargo... ¡Salvador no tiene hermanos!

¿Cómo es esto posible? ¿Por qué asegura Salvador que no tiene ningún hermano?

¡Buena suerte!

Solución del enigma

¿Quieres saber el secreto de este caso? Haz clic en el siguiente enlace para acceder a la solución:

Solución de "El curioso caso de tres socorristas" [Haz clic aquí]

Jacob Sierra Díaz

Cálculo de los ángulos de un triángulo rectángulo

¿Cómo calcular los ángulos de un triángulo rectángulo? Supongamos que queremos hallar la hipotenusa b y los valores de los ángulos A, B y C del siguiente triángulo rectángulo:

Seguramente que la primera duda que nos viene a la cabeza al ver este problema de trigonometría es ¿por dónde empiezo? La respuesta es muy sencilla... ¡Por lo más fácil!

Y lo más fácil es hallar el ángulo B. Este es un ángulo recto, y por lo tanto mide 90º. Recuerda que todos los ángulos rectos siempre miden 90º.

A continuación, vamos a calcular la hipotenusa b. ¿Cómo? Mediante el famoso Teorema de Pitágoras, el cual dice que la hipotenusa al cuadrado es igual a la suma de los catetos elevados (cada uno) al cuadrado [H*H = C*C + C*C]. Entonces, la medida de la hipotenusa la podemos calcular de la siguiente manera:

Ya tenemos todos los lados del triángulo, calculemos ahora el ángulo azul A. ¿Cómo? Con la razón trigonométrica de un ángulo agudo (en un triángulo rectángulo). En concreto, utilizaremos el seno del ángulo agudo A. El seno de un ángulo agudo es igual al cociente entre el cateto opuesto al ángulo (en nuestro caso el que mide 12 unidades) y la hipotenusa (que es la que acabamos de calcular).  Desarrollemos esta fórmula con nuestro ejemplo: 

Con esto, acabamos de calcular el seno del ángulo A. Gracias a este resultado podremos, a continuación, calcular el ángulo A gracias al arcoseno (despejando A). Esta operación, que puede parecer compleja, es en realidad muy sencilla con una calculadora científica. ¡Comprobémoslo!

Ahora solo nos queda calcular el ángulo C. Para ello, tenemos que tener en cuenta una regla muy sencilla llamada ángulos complementarios. Llamamos ángulos complementarios a aquellos que suman 90º. En un triángulo rectángulo los dos ángulos agudos son complementarios porque siempre sumarán 90º. Conocemos B y conocemos A (lo acabamos de calcular), apliquemos la fórmula y despejemos C para calcular el ángulo:

A + C = B; A + C = 90º; 36,80º + C = 90º; C = 90º - 36,86º; C = 53,14º

En conclusión; A = 36,86º; B = 90º; b = 20 unidades; C = 53,14º. ¿No te parece asombroso que solo con dos datos hemos sido capaces de calcular los ángulos del triángulo rectángulo? Pues sean cuales sean los datos de cualquier triángulo, el proceso es igual para todos los triángulos rectángulos.

Jacob Sierra Díaz

SOLUCIÓN. La escalera numérica

El enigma, al que puedes acceder antes de seguir leyendo en el siguiente enlace, nos preguntaba por el siguiente número de una sucesión numérica ordenada con cierta lógica.

La escalera numérica (Clic aquí para acceder al enigma)

La siguiente cifra de la sucesión numérica no sigue una razón numérica. En realidad, tiene que ver más con las letras que componen los números. Así, el siguiente número de la escalera sería 1001 (mil uno). 

¿Por qué? Porque en la escalera están escritos los primeros números (empezando por el 0 de la recta numérica) que no contienen la vocal e: uno, dos, cuatro, cinco, ocho y mil. Por lo que el siguiente número que sigue que no contenga la vocal es es mil uno, y el siguiente sería mil dos.

Este es un enigma curioso que se puede plantear a modo de curiosidad ligüistica-matemática y, que sin lugar a dudas, será motivo de sonrisas. ¡Es increíble el hecho de saber que desde el ocho hasta el mil los números incluyen por lo menos una `e´! ¿verdad?.

Jacob Sierra Díaz

Febrero (2020): el cielo del mes

Durante el mes más corto del año ¿qué podremos ver en nuestros cielos?

Principalmente y, si el tiempo atmosférico acompaña, podremos ver las fases de la Luna los fines de semana. Además, si estás en el hemisferio sur, no te puedes perder las conjunciones de Marte, Júpiter y Saturno con la Luna, siendo este, el evento astronómico del mes. ¡Pero aún hay más cosas que el universo nos quiere enseñar!

Descarga la guía de las efemérides de febrero (2020) para latitudes 40º Norte para no perderte ninguna cita con el cielo este mes, desde las constelaciones más bellas para observar, hasta la posición de los planetas. Puedes acceder y descargar esta guía haciendo clic en la siguiente imagen, que te llevará directamente a una carpeta de Box.

Deseamos que tengas buenos cielos durante este mes.

Jacob Sierra Díaz y AstroCuenca

Sección de Ciencias del Universo